-
Lý thuyết Toán 10 giá trị lượng giác của một cung là một trong những kiến thức quan trọng mà các em cần nắm vững. Do đó, việc nắm vững những nội dung liên quan đến chủ đề này như định nghĩa, hệ quả, công thức cơ bản,… và các dạng bài tập cơ bản là vô cùng quan trọng. Các em hãy cùng TheTips tìm hiểu chi tiết về kiến thức này Toán 10 giá trị lượng giác của một cung qua bài viết dưới đây.
Định nghĩa giá trị lượng giác của một cung
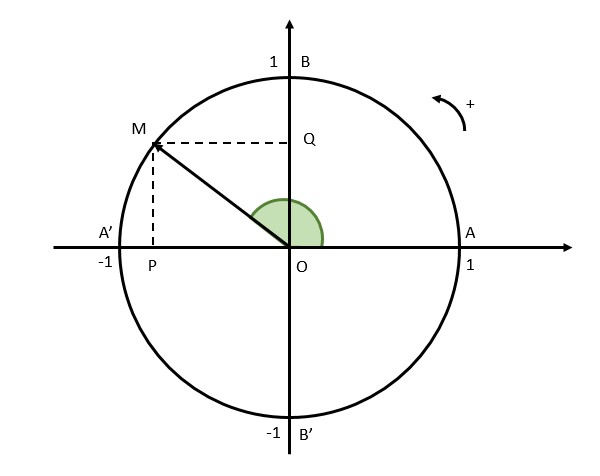
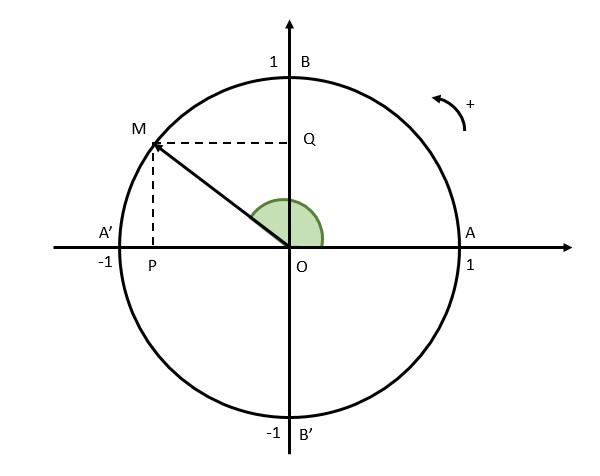
Định nghĩa giá trị lượng giác của một cung (Nguồn: Internet) Trên đường tròn lượng giác tâm O, cho điểm M(x0; y0) sao cho số đo cung AM = α thì:
begin{aligned} &bullet sinα=overline{OQ}=y_0\ &bullet cosα=overline{OP}=x_0\ &bullet tanα = frac{sinα}{cosα} (cosα ≠ 0)\ &bullet cotα = frac{cosα}{sinα} (sinα ≠ 0) end{aligned}Định nghĩa: Các giá trị sinα, cosα, tanα và cotα là các giá trị lượng giác của một cung. Các em có thể gọi trục tung là trục sin, trục hoành là trục cosin.
Ví dụ: Tính cos (-240o)
Hướng dẫn:
Để tính được giá trị lượng giác của cung AM có số đo α bất kỳ, các em tiến hành thực hiện theo các bước sau:
- Biểu diễn cung AM trên đường tròn lượng giác tâm O.
- Xác định tọa độ điểm M, từ đó suy ra các giá trị lượng giác cần tìm.
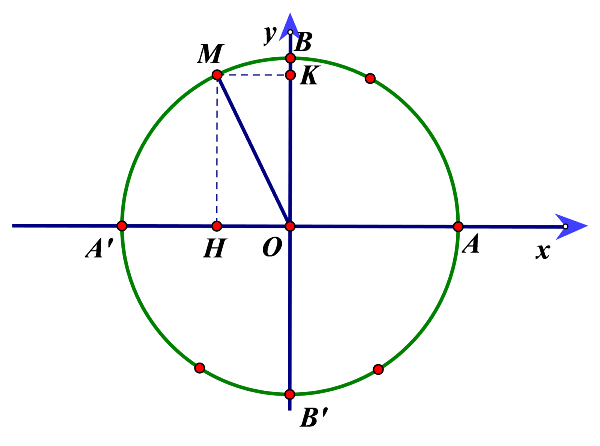
begin{aligned} &text{Ta có: } -240^circ = 120^circ - 360^circ \ &text{Suy ra: }cos(-240^circ)=cos120^circ=-frac{1}{2} end{aligned}Hệ quả giá trị lượng giác của một cung
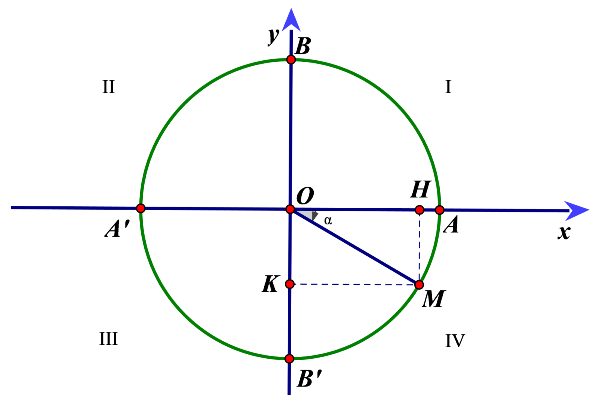
begin{aligned} &small text{1. Với sinα và cosα luôn xác định với mọi giá trị α ∈ R, ta có:}\ &small bull sin (α+ 2kπ) = sinα (⩝k ∈ Z)\ &small bull cos (α+ 2kπ) = cosα (⩝k ∈ Z)\ &small2. -1Giá trị lượng giác của các cung đặc biệt
Một số giá trị lượng giác của các cung đặc biệt để thể hiện thông qua bảng sau:
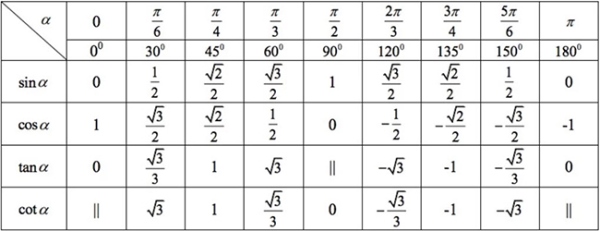
Giá trị lượng giác của các cung có liên quan
Cung đối nhau
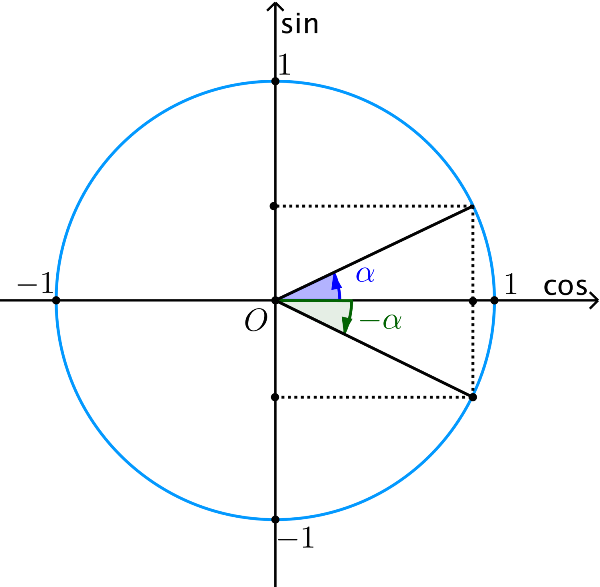
Vì các điểm cuối của hai cung AM, AM’ đối xứng với nhau qua trục hoành, nên ta có:
begin{aligned} &bull sin (-α) = -sinα\ &bull cos (-α) = cosα\ &bull tan (-α) = -tanα\ &bull cot (-α) = -cotα end{aligned}Cung bù nhau
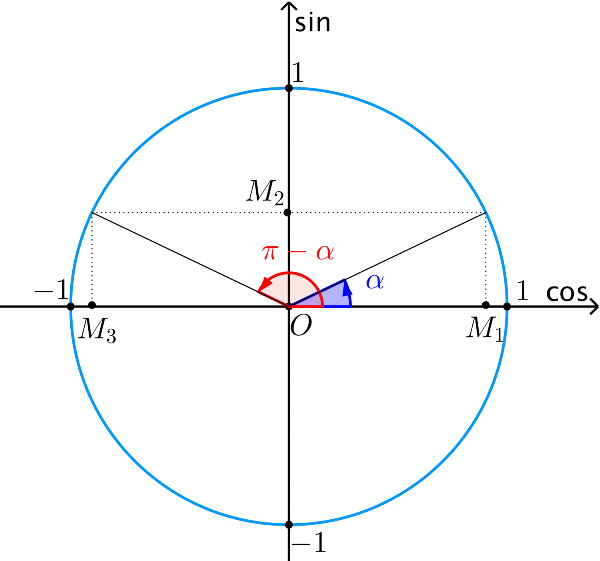
Vì các điểm cuối của hai cung AM, AM’ đối xứng với nhau qua trục tung, nên ta có:
begin{aligned} &bull sin (pi-α) = sinα\ &bull cos (pi-α) = -cosα\ &bull tan (pi-α) = -tanα\ &bull cot (pi-α) = -cotα end{aligned}Cung phụ nhau
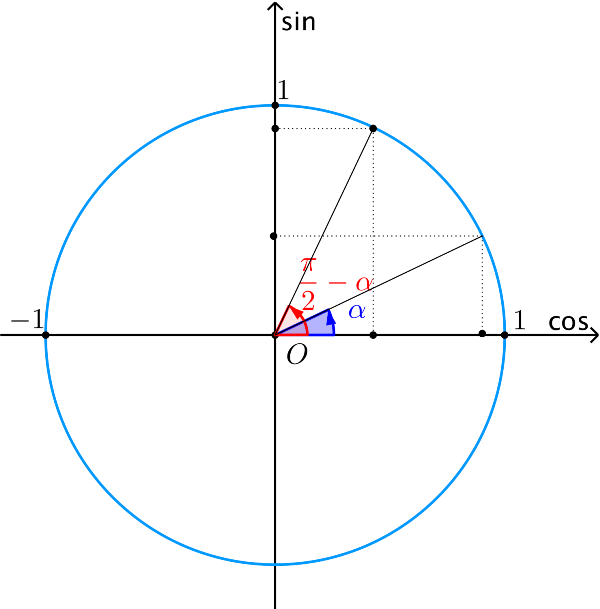
Các điểm cuối của hai cung đối xứng với nhau qua đường phân giác d của góc xOy, nên ta có:
begin{aligned} &bull sin left(frac{pi}{2}-αright) = cosα\ &bull cos left(frac{pi}{2}-αright) = sinα\ &bull tan left(frac{pi}{2}-αright) = cotα\ &bull cot left(frac{pi}{2}-αright) = tanα end{aligned}Cung hơn kém nhau π
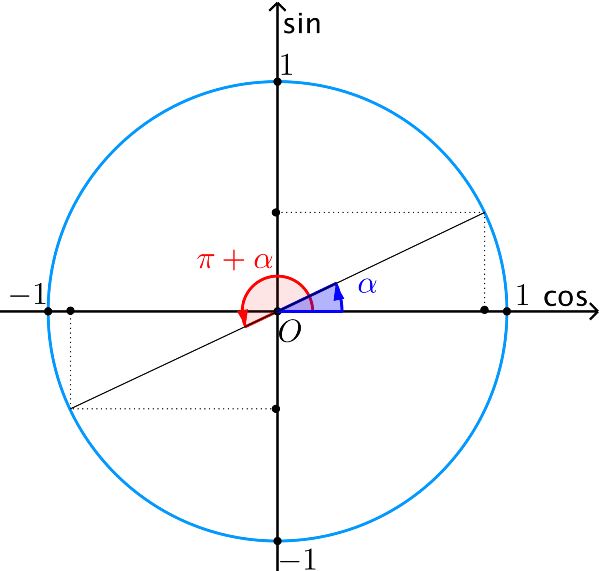
Các điểm cuối của hai cung đối xứng với nhau qua gốc tọa độ O, nên ta có:
begin{aligned} &bull sin (α+pi) = -sinα\ &bull cos(α+pi) = -cosα\ &bull tan(α+pi)= tanα\ &bull cot (α+pi) = cotα end{aligned}Chú ý: Để có thể ghi nhớ các công thức trên một cách dễ dàng, các em có thể học thuộc bí kíp sau “cos đối, sin bù, phụ chéo, tan hơn kém pi”.
Các công thức lượng giác cơ bản
Một số công thức lượng giác cơ bản mà các em có thể tham khảo như:
begin{aligned} &bull sin^2α + cos^2α = 1\ &bull tanα.cotα = 1\ &bull 1 + tan^2α = frac{1}{cos^2α}\ &bull 1 + cot^2α = frac{1}{sin^2α} end{aligned}Ý nghĩa hình học của tan và cotan
Ý nghĩa hình học của tanα
begin{aligned} &small text{Tanα được biểu diễn trong đường tròn lượng giác bởi độ dài đại số của vectơ } overrightarrow{AT} text{ trên trục t’At. }\ &smalltext{Trục t’At được gọi là trục tan.} end{aligned}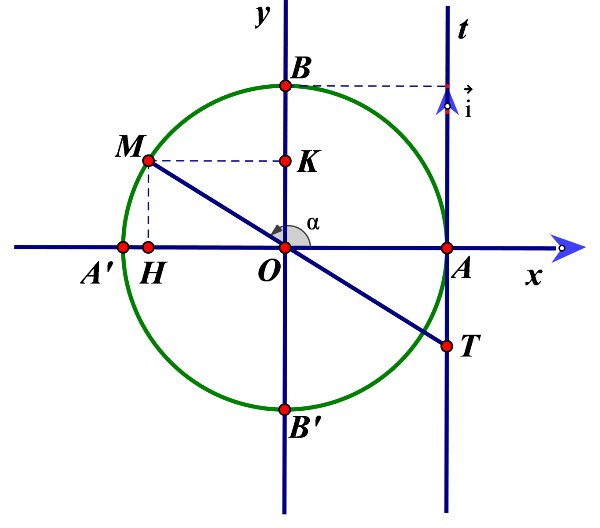
Ý nghĩa hình học của tan (Nguồn: Internet) Ý nghĩa hình học của cotα
begin{aligned} &small text{Cotα được biểu diễn trong đường tròn lượng giác tâm O bởi độ dài đại số của vectơ }overrightarrow{BS} text{ trên trục s’Bs.}\ &smalltext{Trục s’Bs được gọi là trục cot.}\ end{aligned}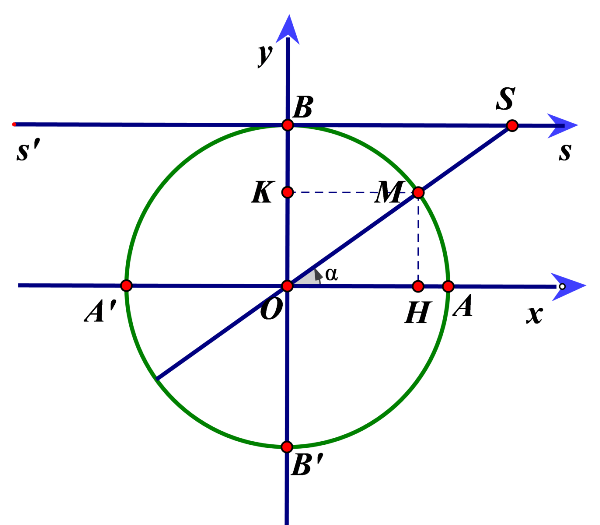
Ý nghĩa hình học của cot (Nguồn: Internet) 4 ví dụ minh họa về giá trị lượng giác của một cung
Ví dụ 1:
text{Cho }sinα = frac{sqrt3}{2} với 0Hướng dẫn:
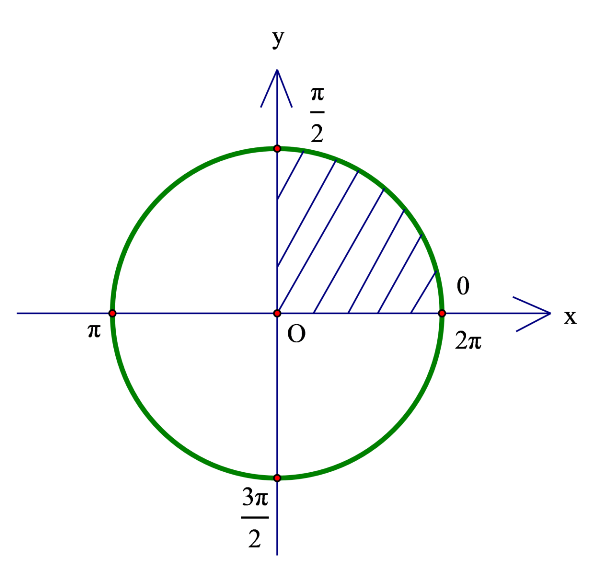
begin{aligned} &text{Ta có: }sin^2α + cos^2α = 1\ &cos^2α = 1 - sin^2α = 1 - left(frac{sqrt{3}}{2}right)^2 = frac{1}{4}\ &text{Vì } 0 0 ⟹ cosα = frac12 end{aligned}Ví dụ 2:
text{Cho }cosα = frac{sqrt{11}}{6} text{ với } frac{3π}{2}Hướng dẫn:
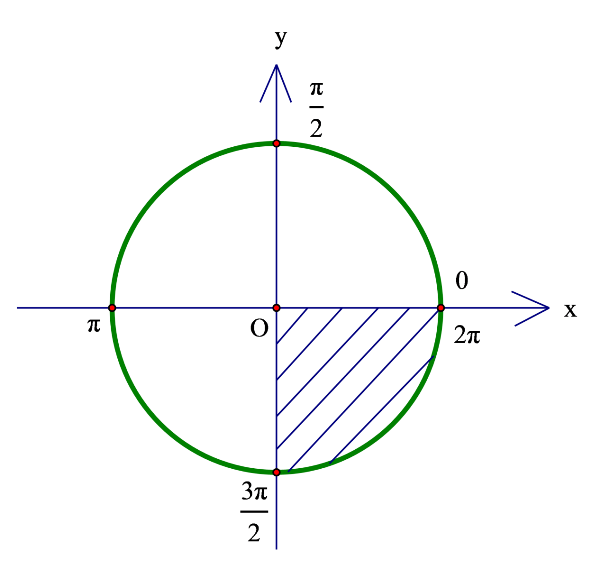
begin{aligned} &text{Ta có: }sin^2α + cos^2α = 1\ &⟹ sin^2α = 1 - cos^2α = 1 - left(frac{sqrt{11}}{6}right)^2 = frac{25}{36} &⟹ sinα = ± frac56\ &text{Vì }frac{3π}{2}Ví dụ 3: Rút gọn biểu thức B sau đây:
B = cos (90o – x).sin (180o – x) – sin (90o – x).cos (180o – x)
Hướng dẫn:
Áp dụng công thức cung bù nhau và cung phụ nhau, ta có:
B = cos (90o – x).sin (180o – x) – sin (90o – x).cos (180o – x)
= sinx.sinx – cosx.(-cosx)
= sin2x + cos2x
= 1
Ví dụ 4:
text{Tính }cos frac{-11π}{4}Hướng dẫn:
begin{aligned} &text{Sử dụng cung đối, ta có: }\ &cos frac{-11π}{4} = cosfrac{11π}{4} = cosleft(2π + frac{3π}{4}right) = cos frac{3π}{4} = cos (π - frac{π}{4}) = - cos frac{π}{4} = - frac{sqrt2}{2} end{aligned}Nguồn: Toán 10 Giá Trị Lượng Giác Của Một Cung – Marathon Education
Lý Thuyết Toán 10 Giá Trị Lượng Giác Của Một Cung
Lý thuyết Toán 10 giá trị lượng giác của một cung là một trong những kiến thức quan trọng mà các em cần nắm vững. Do đó, việc nắm vững những nội dung liên quan đến chủ đề này như định nghĩa, hệ quả, công thức cơ bản,… và các dạng bài tập cơ bản […]
Đã cập nhật 23 tháng 2 năm 2022
Bởi TopOnMedia
Tags:
Marathon