Lý Thuyết Về Tích Phân Và Phương Pháp Tính Tích Phân Cơ Bản

Tích phân là một trong những nội dung quan trọng của chương trình Toán học 12. Nắm chắc lý thuyết, phương pháp tính tích phân cơ bản sẽ giúp các em giải nhanh và chính xác các bài tập liên quan và đạt điểm cao trong các kỳ thi. Vì thế, trong bài viết này, TheTips sẽ giúp các em tìm hiểu chi tiết tích phân là gì và những phương pháp tính tích phân cơ bản thường gặp.

Định nghĩa tích phân

Để học tốt tích phân, trước tiên các em cần nắm vững lý thuyết tích phân là gì. 

Xét hàm số f(x) xác định và liên tục trên đoạn [a;b]. Giả sử F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b] thì F(b) – F(a) chính là tích phân từ a đến b của hàm số f(x), hay còn gọi là tích phân được xác định trên đoạn [a;b]. Cụ thể:

int^b_a f(x)dx=F(x)|^b_a=F(b)-F(a)

Tính chất của tích phân

Để giải các bài toán tích phân, các em cần nắm được những tính chất cơ bản sau của tích phân:

Phương pháp tính tích phân

Khi giải các bài tập tích phân, các em có thể áp dụng nhiều phương pháp khác nhau. Trong đó, 2 phương pháp cơ bản được áp dụng nhiều nhất là đổi biến số và tích phân từng phần.

Phương pháp đổi biến số

Cho hàm số f(x) được xác định và có đạo hàm liên tục trên đoạn [a;b]. Các em có thể sử dụng phương pháp đổi biến số để tính tích phân. Công thức đổi biến số cụ thể:

int^b_af(u)u'(x)dx=int^{u(b)}_{u(a)}f(u)du

Sau đây là các dạng tích phân và cách đổi biến số thường gặp mà các anh chị Marathon đã tổng hợp được. Các em hãy tham khảo và áp dụng để giải bài tập:

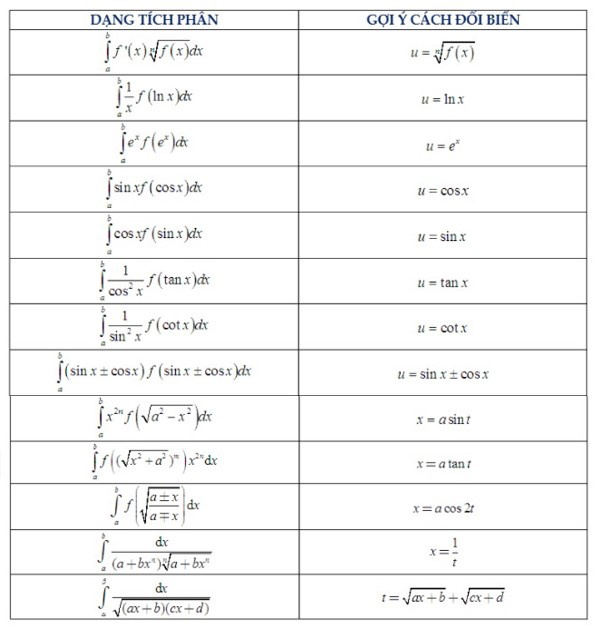
Phương pháp tích phân từng phần

Các em nên áp dụng phương pháp tích phân từng phần để giải nhanh chóng và chính xác những bài tập mà hàm số đã cho thuộc dạng:

• Hàm đa thức – hàm mũ
• Hàm đa thức – hàm lượng giác
• Hàm mũ – hàm lượng giác
• Hàm logarit – hàm đa thức
• …

Công thức tích phân từng phần :

int^b_au(x)v'(x)dx=u(x)v(x)|^b_a-int^b_au'(x)v(x)dx

Các dạng bài tập tích phân cơ bản

Dạng 1: Hàm logarit

Ví dụ: Các em hãy tính tích phân của hàm số:

I=int^1_0e^x(2e^x+1)^3dx

Bài giải:

Ta có:

begin{aligned}
I&=int^1_0e^x(2e^x+1)^3dx\
&=frac{1}{2}int^1_0(2e^x+1)^3d(2e^x+1)\
&=left.frac{1}{2}.frac{(2e^x+1)^4}{4}right|^1_0\
&=frac{1}{2}left[frac{(2e+1)^4}{4}-frac{81}{4} right]\
&=frac{(2e+1)^4}{8}-frac{81}{8}
end{aligned}

Dạng 2: Hàm phân thức

Ví dụ: Các em hãy tính tích phân của hàm số:

I=int^4_3frac{x+1}{x-2}dx

Bài giải:

Ta có:

begin{aligned}
I&=int^4_3frac{x+1}{x-2}dx\
&=int^4_3left(1+frac{3}{x-2}right)dx\
&=[x+3ln(x-2)|^4_3\
&=(4+3ln2)-(3+ln1)\
&=1+3ln2
end{aligned}

Dạng 3: Hàm căn thức

Ví dụ: Các em hãy tính tích phân của hàm số:

I=int^4_0sqrt{2x+1}dx

Bài giải:

Ta có:

begin{aligned}
I&=int^4_0sqrt{2x+1}dx\
&=frac{1}{2}int^4_0sqrt{2x+1}d(2x+1)\
&=left.frac{1}{2}.frac{2}{3}(2x+1)sqrt{2x+1}right|^4_0\
&=9-frac{1}{3}=frac{26}{3}
end{aligned}

Dạng 4: Hàm đa thức

Ví dụ: Các em hãy tính tích phân của hàm số:

I=int^1_0(3x^2+2x-1)dx

Bài giải:

Ta có:

begin{aligned}
I&=int^1_0(3x^2+2x-1)dx\
&=int^1_03x^2dx+int^1_02xdx-int^1_0dx\
&=(x^3+x^2-x)|^1_0=1
end{aligned}

Dạng 5: Hàm lượng giác

Ví dụ: Tính tích phân của hàm số:

I=int^{frac{pi}{2}}_0sin3x.cosxdx

Bài giải: 

Ta có:

begin{aligned}
I&=int^{frac{pi}{2}}_0sin3x.cosxdx\
&=frac{1}{2}int^{frac{pi}{2}}_0(sin4x+sin2x)dx\
&=left.frac{1}{2}left[-frac{1}{4}cos4x-frac{1}{2}cos2xright]right|^{frac{pi}{2}}_0\
&=frac{1}{2}left[-frac{1}{4}(cos2pi-cos0)-frac{1}{2}(cospi-cos0)right]\
&=frac{1}{2}left[-frac{1}{4}(1-1)-frac{1}{2}(-1-1)right]=frac{1}{2}
end{aligned}

Nguồn: Tích Phân – Marathon Education