Cách Tìm Tập Xác Định Và Điều Kiện Hàm Số Mũ

Hàm số mũ và hàm logarit là những kiến thức Toán thường gặp trong chương trình cấp 3. Để giải được các bài toán này, các em phải nắm vững các công thức tính từng loại hàm số mũ cũng như thực hành nhiều với các dạng bài khác nhau. Bài viết sau của TheTips sẽ tổng hợp và chia sẻ đến các em lý thuyết và cách giải bài tập liên quan đến tập xác định và điều kiện hàm số mũ.

Mục lục

1 Hàm số mũ là gì?
2 Tính chất của hàm số mũ
3 Tập xác định và điều kiện hàm số mũ
4 Bài tập minh họa và lời giải

Hàm số mũ là gì?

Hàm số mũ là hàm số có dạng: y = a^x với a là số dương khác 1.

Tính chất của hàm số mũ
- Đạo hàm của hàm số: ∀ x ∈ R, y’ = a^xlna
- Chiều biến thiên của hàm số:
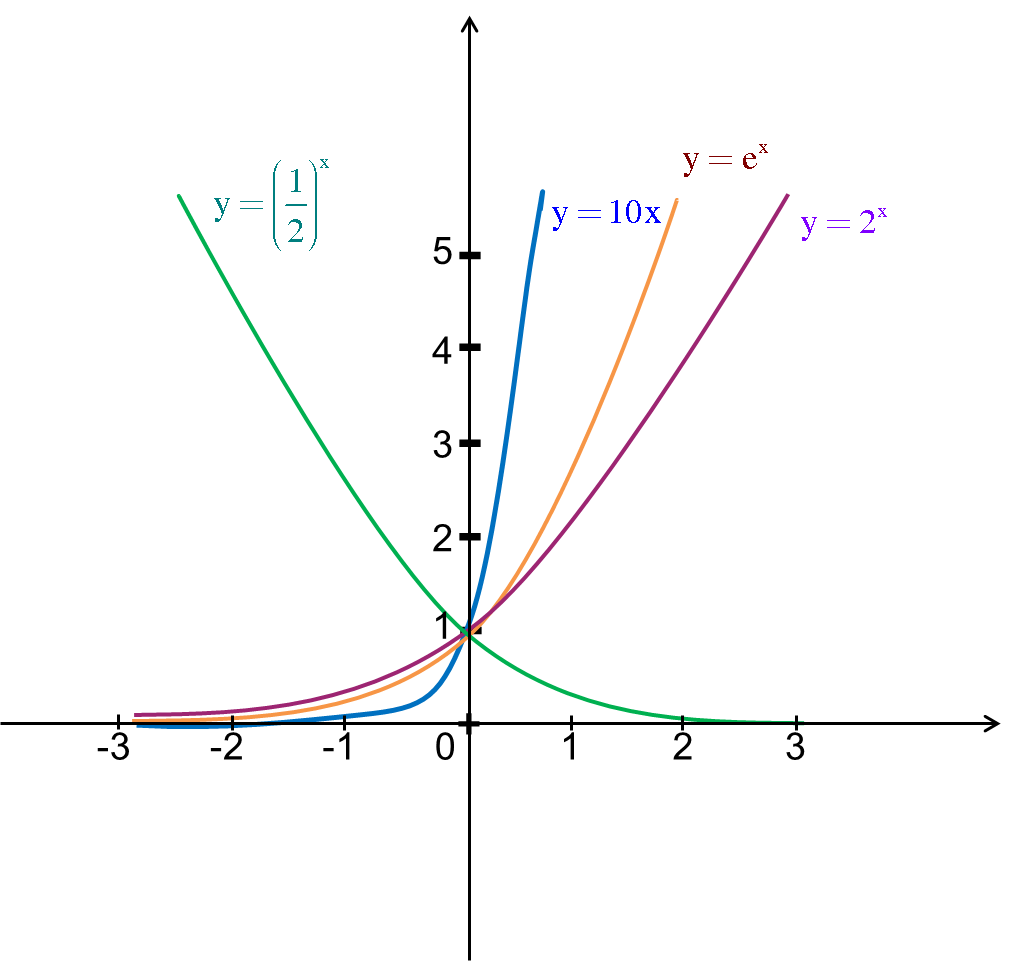
- Hàm số luôn đồng biến nếu a > 1
- Hàm số luôn nghịch biến nếu 0
- Đường tiệm cận: Hàm số mũ y = a^x nhận trục Ox làm tiệm cận ngang.
- Vị trí đồ thị: Nằm hoàn toàn về phía trên của trục hoành, y = a^x > 0 ∀ x. Hàm số luôn cắt trục Oy tại điểm (0;1) và đi qua điểm (1;a).
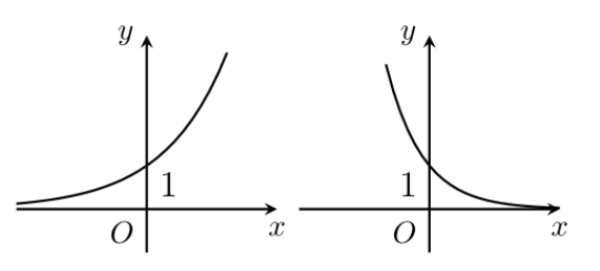
Đồ thị hàm số mũ (Nguồn: Internet)

Tập xác định và điều kiện hàm số mũ

Hàm số mũ y = a^x với a > 0, a ≠ 1 có tập xác định là R.

Đối với các bài tìm tập xác định dạng phức tạp y = a^u(x), ta chỉ cần tìm điều kiện hàm số mũ để u(x) xác định.

Bài tập minh họa và lời giải

Để hiểu và nắm vững phương pháp giải bài toán liên quan đến hàm số mũ, các em hãy theo dõi những ví dụ về cách tìm tập xác định và điều kiện của hàm số mũ dưới đây:

Ví dụ 1: Tìm tập xác định của hàm số sau:

y=( x²– 1)^-8

Bài giải:

Hàm số xác định khi và chỉ khi x²– 1 khác 0.
```
begin{aligned}
&x^2-1not=0\
&Leftrightarrow x^2≠ 1\
&Leftrightarrow  x ≠ ±1
end{aligned}
```
Từ đó, ta suy ra tập xác định của hàm số là:

D: R{-1;1}

Ví dụ 2: Tìm tập xác định của hàm số sau:
```
y=(1-2x)^{sqrt3-1}
```
Bài giải:

Hàm số được xác định khi và chỉ khi hàm số này có nghĩa.

Để hàm số có nghĩa thì:
```
1 - 2x > 0 Leftrightarrow x
```
Vậy tập xác định của hàm số trên là:
```
D= (-∞;frac{1}{2})
```
Ví dụ 3: Tìm tập xác định của hàm số sau:
```
y=sqrt{frac{x^2-3x+2}{3-x}}+(2x-5)^{sqrt7 +1}-3x-1
```
Bài giải:

Ta thấy hàm số trên có chứa căn thức của phân số, do vậy để hàm này có nghĩa ta xét các điều kiện như sau:
```
begin{cases}frac{x^2-3x+2}{3-x} geq 0\2x-5>0end{cases}
Leftrightarrow
begin{cases}left[begin{array}{c}xleq1\2leq xfrac{5}{2}end{cases}
Leftrightarrowfrac{5}{2}
```
Từ đó suy ra tập xác định của hàm số là:
```
D=left(frac{5}{2}; 3 right)
```
Nguồn: Điều Kiện Hàm Số Mũ – Marathon Education

Tags:

Marathon

Cách Tìm Tập Xác Định Và Điều Kiện Hàm Số Mũ

Hàm số mũ là gì?

Tính chất của hàm số mũ

Tập xác định và điều kiện hàm số mũ

Bài tập minh họa và lời giải

Đọc Tiếp