Lý Thuyết Toán 12 Cực Trị Của Hàm Số Và Phương Pháp Tìm Cực Trị

Toán 12 cực trị của hàm số là phần nội dung quan trọng trong kỳ thi tốt nghiệp THPT và thi đại học. Do đó, các em cần nắm rõ và vững lý thuyết này để vận dụng vào làm bài tập nhanh chóng, chính xác. Team TheTips đã tổng hợp, biên soạn nội dung cực trị của hàm số và phương pháp tìm cực trị một cách chi tiết, dễ hiểu và chia sẻ đến các em trong bài viết sau.

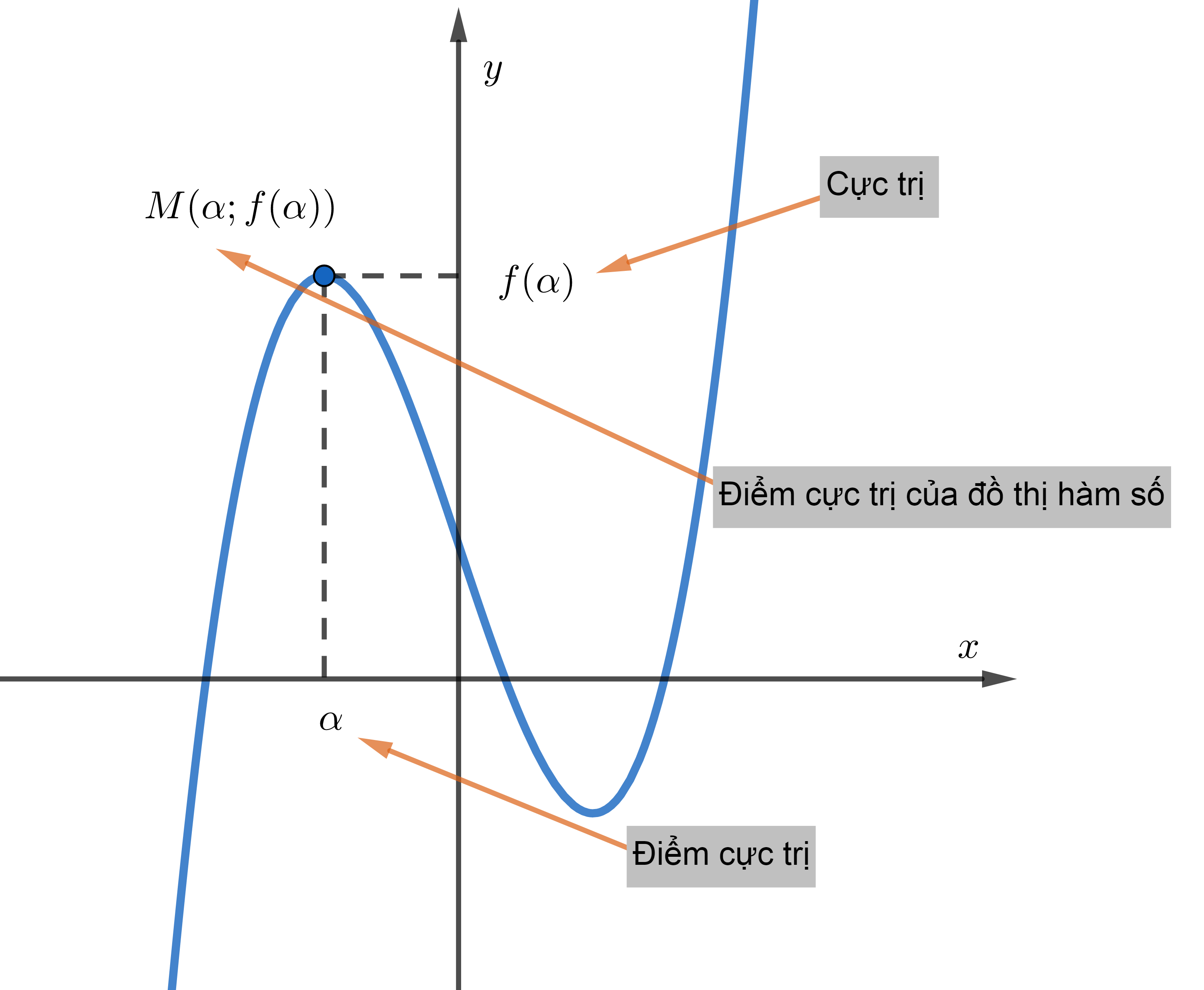
Định nghĩa cực trị của hàm số

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là -∞; b là +∞) và điểm x₀ ∈ (a;b).

Có 2 trường hợp sẽ xảy ra:

• Nếu tồn tại số h > 0 sao cho f(x) 0) với mọi x ∈ (x₀ – h; x₀ + h) và x ≠ x₀ thì ta nói hàm số f(x) đạt cực đại tại x₀.
• Nếu tồn tại số h > 0 sao cho f(x) > f(x₀) với mọi x ∈ (x₀ – h; x₀ + h) và x ≠ x₀ thì ta nói hàm số f(x) đạt cực tiểu tại x₀.

Điều kiện để hàm số có cực trị

Giả sử hàm số y = f(x) liên tục trên K = (x₀ – h; x₀ + h) và có đạo hàm trên K hoặc trên K {x₀}, với h > 0.

Có 2 trường hợp là:

• Nếu f'(x) > 0 trên khoảng (x₀ – h; x₀) và f'(x) 0; x₀ + h) thì x_o là một điểm cực đại của hàm số f(x).
• Nếu f'(x) 0 – h; x₀) và f'(x) > 0 trên (x₀; x₀ + h) thì x₀ là một điểm cực tiểu của hàm số f(x).

Phương pháp tìm cực trị của hàm số

Để tìm cực trị của hàm số Toán 12 một cách chính xác và nhanh chóng, các em hãy áp dụng những phương pháp sau:

Dựa vào bảng biến thiên

• Bước 1. Tìm tập xác định của hàm số.
• Bước 2. Tính f'(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
• Bước 3. Lập bảng biến thiên.
• Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.

Xét dấu đạo hàm của hàm số

• ​​Bước 1. Tìm tập xác định của hàm số.
• Bước 2. Tính f'(x). Giải phương trình f'(x) và ký hiệu x_i (i = 1; 2; 3;…) là các nghiệm của nó.
• Bước 3. Tính f”(x) và f”(x_i).
• Bước 4. Dựa vào dấu của f”(x_i) suy ra tính chất cực trị của điểm x_i.

Ví dụ minh họa 

Các em cùng theo ví dụ minh hoạ sau đây để hiểu hơn về nội dung Toán 12 cực trị của hàm số khi tìm điểm cực đại, cực tiểu và vẽ bảng biến thiên.

Đề bài:

Tìm các điểm cực đại, cực tiểu của hàm số sau:

y=frac{1}{3}x^3-x^2-3x+frac{3}{4}

Bài giải:

begin{aligned}
&text{Hàm số có TXĐ: D}= R\
&y’= x^2 - 2x - 3\
&y'=0 Leftrightarrow left[ begin{array}{c}    x=-1\
x=3 end{array} right.
end{aligned}

Bảng biến thiên:

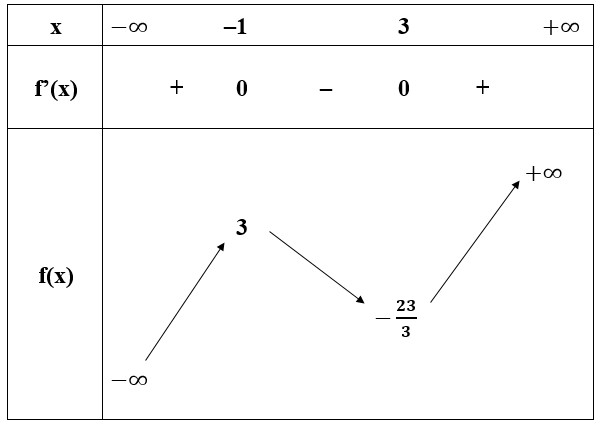
small text{Vậy giá trị cực đại của hàm số là 3 tại }x=-1 text{ và giá trị cực tiểu của hàm số là }frac{-23}{3}text{ tại }x=3.

Nguồn: Toán 12 Cực Trị Của Hàm Số – Marathon Education