Lý Thuyết Toán 10 Hàm Số: Hàm Số Bậc Nhất Và Hàm Số Bậc Hai

Trong lý thuyết Toán 10 hàm số, hàm số bậc nhất và hàm số bậc hai là các kiến thức Toán học cơ bản nhưng quan trọng ở bậc THPT. Do đó, các em nên nắm rõ lý thuyết và làm bài tập nhiều để có thể “xử nhanh diệt gọn” các bài toán liên quan đến nội dung này. Dưới đây, TheTips đã biên soạn và gửi đến các em bài viết về lý thuyết hàm số bậc nhất và bậc hai đầy đủ và chi tiết nhất. Mong rằng bài viết này sẽ có ích cho các em trong quá trình học tập.

Khái quát về hàm số

Định nghĩa

Giả sử có 2 đại lượng x và y, trong đó x là giá trị thuộc tập số D.

Với mỗi giá trị x thuộc tập số D thì ta chỉ có một và chỉ một giá trị tương ứng y thuộc tập số thực ℝ. Từ đó, ta có một hàm số (với x là biến số, y là hàm số của x, D là tập xác định của hàm số).

Tập xác định của hàm số

Tập xác định của hàm số y = f(x) chính là tập hợp tất cả các số thực x ∈ ℝ, sao cho biểu thức f(x) có nghĩa.

Ví dụ: Tìm tập xác định của hàm số y = f(x) = 2x -3

Bài giải: Điều kiện xác định của hàm số là: 2x – 3 ≥ 0 ⇔ x ≥ 32

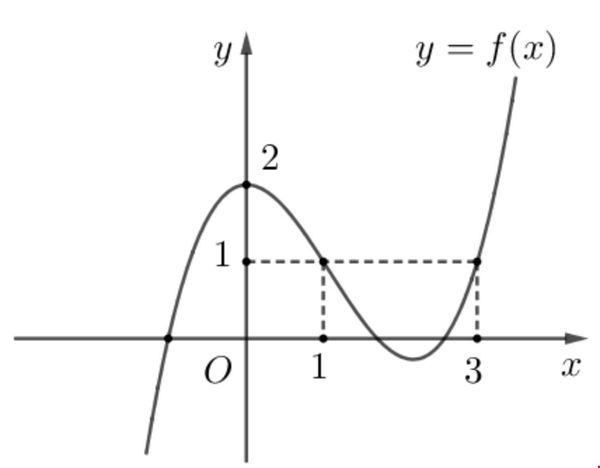
Sự biến thiên của hàm số

• Hàm số y = f(x) đồng biến trên khoảng từ a đến b nếu:

∀ x₁, x₂ ∈ (a,b) : x₁2 ⇨ f(x₁) 2)

• Hàm số y = f(x) nghịch biến trên khoảng từ a đến b nếu:

∀ x₁, x₂ ∈ (a,b) : x₁2 ⇨ f(x₁) > f(x₂)

Tính chẵn lẻ của hàm số

• Với tập xác định D, đồ thị hàm số y = f(x) gọi là hàm số chẵn nếu:

∀ x ∈ D thì -x ∈ D và f(-x) = f(x)

• Với tập xác định D, đồ thị hàm số y = f(x) gọi là hàm số lẻ nếu:

∀ x ∈ D thì -x ∈ D và f(-x) = -(f(x))

Lý thuyết toán 10 về hàm số bậc nhất

Định nghĩa

Hàm số bậc nhất được hiểu là hàm số có dạng: y = ax + b. Trong đó, a và b là các số đã cho (a ≠ 0 và x là biến số).

Tính biến thiên

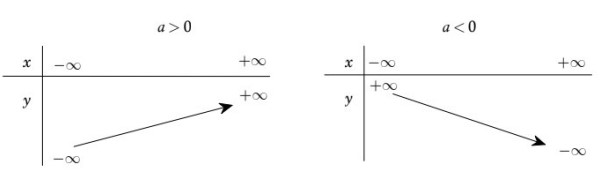
Hàm số bậc nhất y = ax + b (a ≠ 0) có tập xác định D = ℝ, đồng biến trên ℝ nếu a > 0 và nghịch biến trên ℝ nếu a

Bảng biến thiên của hàm số bậc nhất được thể hiện ở bảng sau:

Đồ thị của hàm số

Đồ thị hàm số bậc nhất y = ax + b (a ≠ 0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b, song song với đường thẳng y = ax (b ≠ 0) và trùng với đường thẳng y = ax (b = 0).

Cách vẽ đồ thị hàm số đồ thị hàm số bậc nhất:

• Khi b = 0 thì đồ thị hàm số y = ax là đường thẳng đi qua gốc tọa độ O (0;0) và điểm A (1;a) đã biết.
• Trong trường hợp y = ax + b (a ≠ 0, b ≠ 0) thì đồ thị hàm số y = ax + b là một đường thẳng. Vì vậy, các em chỉ cần xác định được hai điểm phân biệt nào đó của đồ thị rồi vẽ đường thẳng đi qua hai điểm đó. Cụ thể:
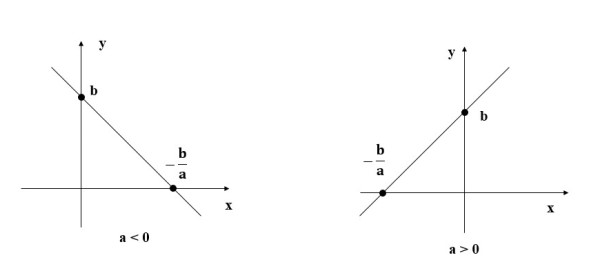
  • Xác định giao điểm của đồ thị hàm số với hai trục của tọa độ. Cho x = 0, tính được y = b và ta có điểm A (0;b). Cho y = 0, tính được x = – ba và ta có điểm B (- ba;0).
  • Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị hàm số y = ax + b có dạng như sau:

Lý thuyết toán 10 về hàm số bậc hai

Định nghĩa

Hàm số bậc hai được cho bởi công thức: y = ax² + bx + c (a ≠ 0) có tập xác định là D = ℝ và biệt thức △ = b² – 4ac.

Tính biến thiên

Chiều biến thiên

begin{aligned}
&footnotesizebulltext{Nếu a > 0 thì hàm số bậc hai }y=ax^2+bx+c text{ đồng biến trên khoảng }\
&footnotesizeleft(-frac{b}{2a};+infinright) text{ và nghịch biến trên khoảng }left(-infin;-frac{b}{2a}right). text{ Điểm cực tiểu của }\
&footnotesize text{hàm số có tọa độ là }left(-frac{b}{2a};-frac{Delta}{4a}right)\
&footnotesizebulltext{Nếu a 

Bảng biến thiên

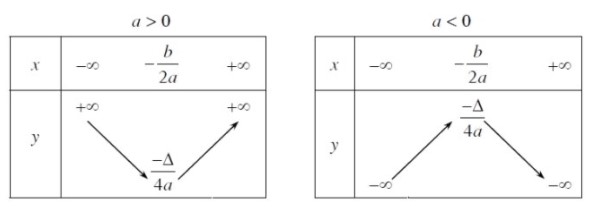
Đồ thị của hàm số

Đồ thị hàm số bậc hai y = ax² + bx + c (a ≠ 0) là đường cong parabol có:

begin{aligned}
&footnotesizebulltext{ Đỉnh là điểm I}left(-frac{b}{2a};-frac{Delta}{4a}right).\
&footnotesizebulltext{ Trục đối xứng là đường thẳng }x=-frac{b}{2a}.\
&footnotesizebulltext{Giao điểm với trục tung là A (0;c).}\
&footnotesizebulltext{Bề lõm của đường cong parabol hướng lên trên nếu a > 0 và hướng xuống }\
&footnotesizetext{dưới khi a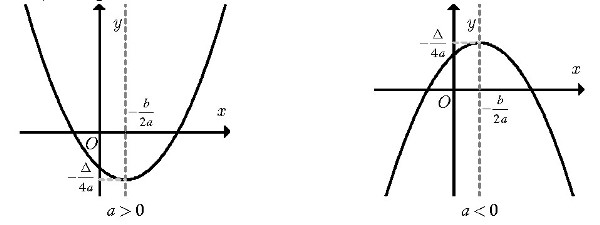 

Cách vẽ đồ thị hàm số

Các em có thể tiến hành vẽ đồ thị hàm số bậc hai theo các bước sau:

• Bước 1: Xác định tọa độ đỉnh I
• Bước 2: Vẽ trục đối xứng
• Bước 3: Xác định tọa độ các giao điểm của Parabol với trục hoành và trục tung (nếu có).
• Bước 4: Vẽ parabol và đặc biệt lưu ý đến dấu của hệ số a.

Nguồn: Toán 10 Hàm Số – Marathon Education