Lý thuyết trong không gian với hệ trục tọa độ oxyz và các dạng thường gặp

Trong chương trình toán hình của THPT, dạng toán trong không gian với hệ tọa độ oxyz thường xuất hiện trong rất nhiều đề thi. Để giải được các bài tập ở dạng này đòi hỏi các em phải ghi nhớ kỹ các công thức của từng dạng để áp dụng. Cùng theo dõi bài viết này để hệ thống lại các kiến thức cần nắm nhé.

Các khái niệm và ký hiệu trong không gian với hệ trục tọa độ oxyz

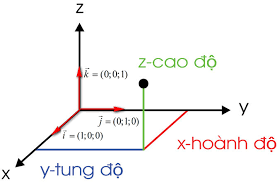
– Hệ trục tọa độ (hay hệ tọa độ trong không gian) được ký hiệu là Oxyz. Các vecto đơn vị i, j, k tương ứng với các trục Ox, Oy, Oz. Trong đó, điểm O được gọi là gốc của hệ tọa độ, Ox  là trục hoành, Oy là trục tung và Oz là trục cao. Các đẳng thức của vecto trong không gian Oxyz:

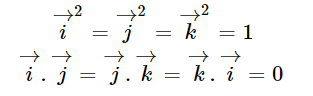
– Các mặt phẳng đi qua 2 trong số các trục tọa độ trên gọi là các mặt phẳng tọa độ, ký hiệu là (Oxy), (Oyz), (Ozx).

Các công thức trong không gian với hệ trục tọa độ oxyz

Tọa độ vecto

Trong không gian oxyz với các vecto cho trước và vecto u. Khi đó tồn tại bộ 3 số duy nhất (x; y; z) sao cho

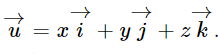
Bộ 3 số đó được gọi là tọa độ của vecto u trong hệ trục tọa độ oxyz. 

Theo định nghĩa hệ tọa độ vecto ta có các tính chất sau:

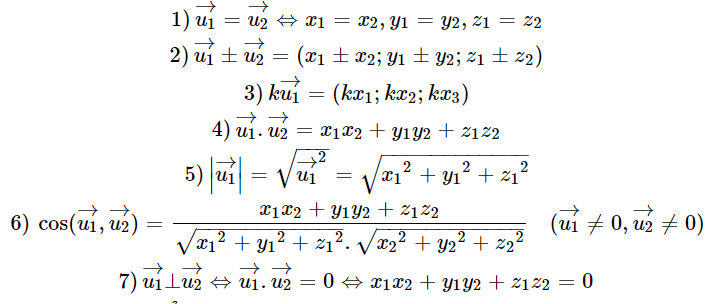
Tọa độ của điểm

Trong không gian oxyz, mỗi điểm M được xác định bởi vecto OM. Do đó nếu (x; y; z) là tọa độ của vecto OM thì nó cũng chính là tọa độ điểm M. Ký hiệu là M=(x; y; z)  hoặc M(x; y; z). Ta có đẳng thức: hình 4

Liên hệ giữa tọa độ vecto và tọa độ 2 điểm mút

Với 2 điểm A, B cho trước ta có:

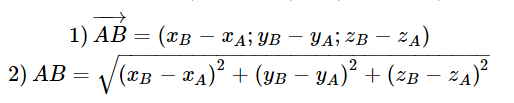
Tích có hướng của 2 vecto 

Tính chất tích có hướng của 2 vecto như sau:

Phương trình mặt cầu

Trong không gian oxyz, cho mặt cầu tâm I(x0; y0; z0) và bán kính R. Mặt cầu có phương trình:

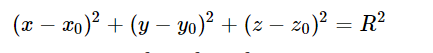
Khi đó mặt cầu có tâm I(−a;−b;−c) với bán kính 

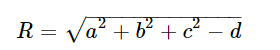
Một số bài tập ứng dụng trong không gian với trục tọa độ oxyz

Bài 1: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng song song với (Oyz) và đi qua điểm A(4; 2; -5). Tìm phương trình của mặt phẳng đã cho.

Bài 2: Trong không gian với hệ trục tọa độ Oxyz cho 2 mặt phẳng: 

(M): x + 3z + 2= 0 và (N): x + 3x – 4 = 0. viết phương trình mặt phẳng song song và cách đều (M), (N).

Bài 3: Trong không gian Oxyz, cho 2 điểm A(-1;-1;2) và B(-1;-1;0). Viết phương trình mặt cầu (S) có đường kính AB. 

Bài 4: Trong không gian với hệ tọa độ Oxyz cho mặt cầu (S): 

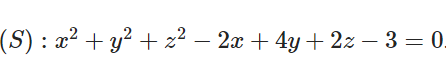
Xác định bán kính R của mặt cầu (S).

Bài viết này đã tổng hợp các công thức trong không gian với hệ trục tọa độ oxyz và các bài tập vận dụng cơ bản. Các em có thể kết hợp giải thêm nhiều dạng bài khác nhau từ dễ đến khó để thành thạo dạng toán này. Chúc các em ôn tập tốt.

Nguồn tham khảo: toan.hoctainha.vn