-
Hình học không gian vẫn luôn là một trong những dạng toán làm khó nhiều thế hệ học sinh. Bên cạnh việc nắm vững lý thuyết, các em còn phải biết cách vẽ hình thật chuẩn xác thì mới có thể giải quyết được loại bài tập hóc búa này. Để giúp các em nắm vững phần kiến thức quan trọng nói trên, hãy cùng TheTips điểm qua 13 dạng toán hình học không gian thường gặp cũng như cách giải chi tiết qua bài viết bên dưới.
Mục lụcDạng 1: Tìm giao tuyến của hai mặt phẳng

Tìm giao tuyến của hai mặt phẳng (Nguồn: Internet) Để tìm giao tuyến của hai mặt phẳng, các em có thể áp dụng 1 trong 2 cách sau:
- Cách 1: Tìm 2 điểm chung giữa hai mặt phẳng
- Điểm chung thứ nhất: Thường là điểm đề cho sẵn, dễ thấy.
- Điểm chung thứ hai: Mỗi mặt phẳng tìm một đường thẳng sao cho cả hai đường thẳng này đều nằm trên cùng một mặt phẳng thứ ba nhưng không song song. Giao điểm của hai đường thẳng chính là điểm chung cần tìm.
Nối hai điểm chung, các em sẽ tìm được giao tuyến của hai mặt phẳng.
- Cách 2: Nếu hai mặt phẳng đã cho chứa hai đường thẳng song song với nhau thì giao tuyến cần tìm chính là đường thẳng đi qua điểm chung và song song với hai đường thẳng này.
Dạng 2: Tìm giao điểm của đường thẳng và mặt phẳng
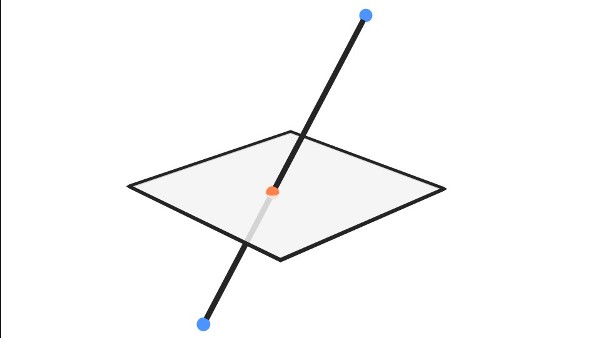
Tìm giao điểm của đường thẳng và mặt phẳng (Nguồn: Internet) Tìm giao điểm của đường thẳng a và mặt phẳng (P) trong hình học không gian tức là tìm giao điểm của đường thẳng a với một đường thẳng b thuộc mặt phẳng (P).
Nếu không tìm ra được đường thẳng b này, các em hãy làm theo các bước sau:
- Bước 1: Tìm một mặt phẳng (Q) chứa đường thẳng a.
- Bước 2: Tìm giao tuyến b giữa 2 mặt phẳng (P) và (Q).
- Bước 3: Tìm giao điểm giữa đường thẳng a và giao tuyến b.
Dạng 3: Chứng minh 3 điểm thẳng hàng
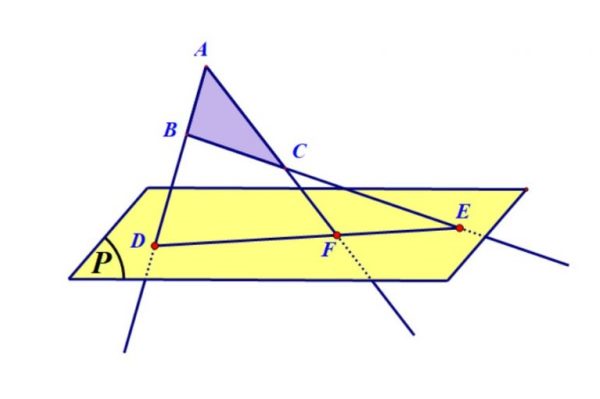
Chứng minh 3 điểm thẳng hàng trong hình học không gian (Nguồn: Internet) Để chứng minh 3 điểm thẳng hàng trong hình học không gian, các em chỉ cần chứng minh 3 điểm này nằm trên giao tuyến của hai mặt phẳng riêng biệt.
Dạng 4: Chứng minh 3 đường thẳng đồng quy
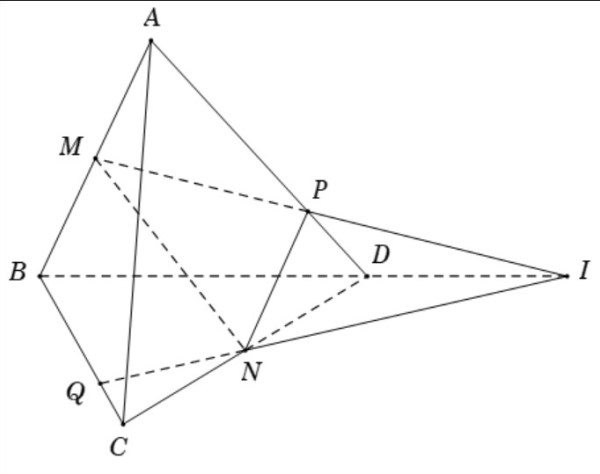
Chứng minh 3 đường thẳng đồng quy (Nguồn: Internet) Khi gặp dạng toán chứng minh 3 đường thẳng đồng quy trong hình học không gian, các em có thể chứng minh bằng 2 cách sau:
- Cách 1: Tìm giao điểm 2 đường thẳng nằm trên hai mặt phẳng riêng biệt. Sau đó chứng minh giao tuyến của hai mặt phẳng này chính là đường thẳng thứ 3.
- Cách 2: Chứng minh 3 đường thẳng đều thuộc các mặt phẳng riêng biệt và cắt nhau từng đôi một.
Dạng 5: Tìm tập hợp giao điểm của 2 đường thẳng
Đối với bài toán tìm tập hợp giao điểm của 2 đường thẳng, các em hãy vận dụng kiến thức hình học không gian để giải lần lượt theo các bước như sau:
- Bước 1: Tìm mặt phẳng (P) cố định chứa đường thẳng a.
- Bước 2: Tìm mặt phẳng (Q) cố định chứa đường thẳng b.
- Bước 3: Tìm giao tuyến c của hai mặt phẳng (P) và (Q). Tập hợp giao điểm cần tìm thuộc giao tuyến c.
- Bước 4: Giới hạn.
Dạng 6: Dựng thiết diện của mặt phẳng và khối đa diện
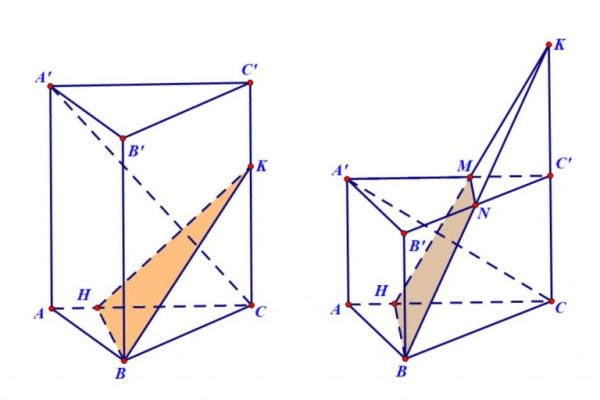
Dựng thiết diện của mặt phẳng và khối đa diện (Nguồn: Internet) Dạng bài dựng thiết diện của mặt phẳng và khối đa diện sẽ trở nên đơn giản hơn khi các em làm theo cách giải dưới đây:
- Tìm đoạn giao tuyến của mặt phẳng với các mặt của khối đa diện:
- Đầu tiên, các em hãy tìm giao tuyến của mặt phẳng với một mặt của khối đa diện.
- Sau đó, các em kéo dài giao tuyến này sao cho cắt các cạnh thuộc mặt này của khối đa diện.
- Các em làm tương tự với các mặt khác của khối đa diện cho đến khi các giao tuyến khép kín.
- Loại bỏ các đoạn thẳng bên ngoài khối đa diện, các em sẽ được thiết diện cần dựng.
Dạng 7: Chứng minh một đường thẳng đi qua một điểm cố định
Nếu các em gặp dạng bài tập hình học không gian này thì cũng đừng quá lo lắng. Các em hãy áp dụng phương pháp dưới đây để giải quyết dạng bài tập này một cách “nhanh, gọn, lẹ”:
- Chứng minh đường thẳng a là giao tuyến của hai mặt phẳng (P) và (Q).
- Mặt phẳng (P) cố định, mặt phẳng (Q) di động quanh một đường thẳng b.
- Tìm giao điểm I của mặt phẳng (P) và b.
- Suy ra được đường thẳng a đi qua điểm cố định I.
Dạng 8: Chứng minh 2 đường thẳng song song
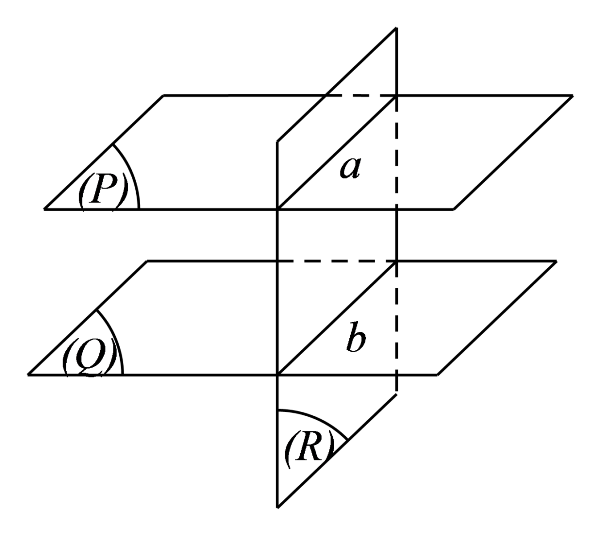
hứng minh 2 đường thẳng song song (Nguồn: Internet) Đối với dạng bài chứng minh 2 đường thẳng song song trong hình học không gian, có 3 cách giải thông dụng mà các em có thể áp dụng như sau:
- Cách 1: Chứng minh đường thẳng a và b đồng phẳng. Sau đó, áp dụng các phương pháp thường dùng để chứng minh song song trong hình học phẳng. Ví dụ như định lý Talet, sử dụng đường trung bình,…. Cuối cùng các em có thể kết luận a // b.
- Cách 2: Sử dụng một đường thẳng thứ 3 là c. Chứng minh a và b song song với đường thẳng này. Theo tính chất bắc cầu, các em sẽ suy ra được a // b.
- Cách 3: Vận dụng định lý của đường giao tuyến “Nếu hai mặt phẳng cắt nhau và lần lượt chứa hai đường thẳng song song cho trước thì giao tuyến của chúng sẽ cùng phương với 2 đường thẳng ấy.”
Dạng 9: Tìm góc giữa 2 đường thẳng chéo nhau
Dạng toán tìm góc giữa 2 đường thẳng chéo nhau cũng thường thấy khi học hình học không gian. Để giải được loại bài tập này, các em chỉ cần sử dụng phương pháp đơn giản như sau:
- Bước 1: Lấy 1 điểm O tại 1 vị trí tùy ý.
- Bước 2: Qua điểm O vừa chọn, lần lượt vẽ c // a, d // b.
- Bước 3: Góc nhọn tạo thành giữa 2 đường thẳng c và d chính là góc giữa 2 đường thẳng chéo nhau mà ta đang cần tìm.
Dạng 10: Chứng minh đường thẳng song song với mặt phẳng
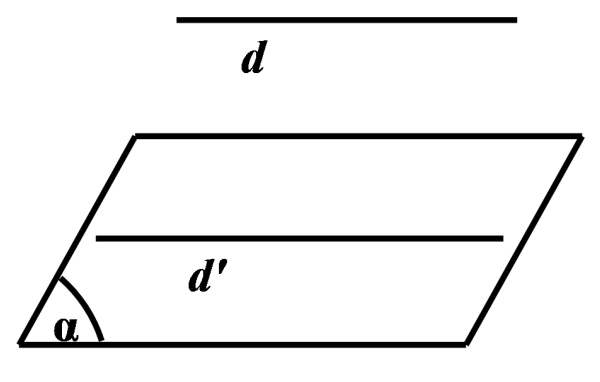
Chứng minh đường thẳng song song với mặt phẳng (Nguồn: Internet) Đối với dạng bài tập này, hãy áp dụng 1 trong 2 cách dưới đây:
- Cách 1: Tiến hành chứng minh a song song với một đường thẳng b bất kì thuộc mặt phẳng (P). Nếu chưa tìm được b, các em hãy làm tuần tự các bước như sau:
- Bước 1: Tìm một mặt phẳng (Q) có chứa a, (Q) không song song với (P).
- Bước 2: Tìm b = (P) ∩ (Q).
- Bước 3: Tiến hành chứng minh a // b.
- Cách 2: Chứng minh a thuộc (Q) // (P).
Dạng 11: Dựng thiết diện song song với một đường thẳng cho trước
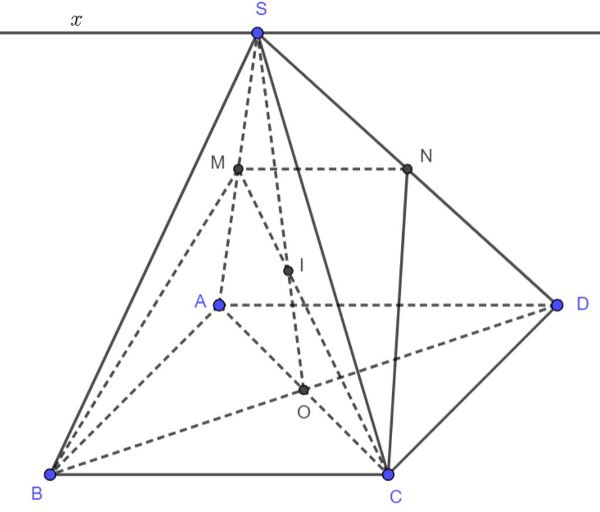
ựng thiết diện song song với một đường thẳng cho trước (Nguồn: Internet) Dựng thiết diện song song với một đường thẳng cho trước (Nguồn: Internet)
Dựng thiết diện song song với một đường thẳng cho trước trong hình học không gian không quá khó. Các em hãy dựa vào tính chất: Mặt phẳng song song với đường thẳng a, nếu cắt mặt phẳng nào chứa a thì sẽ cắt theo giao tuyến song song với a để “công phá” dạng bài tập này.
Dạng 12: Chứng minh 2 mặt phẳng song song
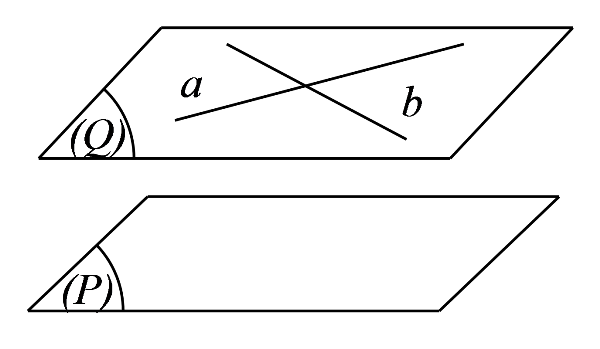
Chứng minh hai mặt phẳng song song (Nguồn: Internet) Chứng minh 2 mặt phẳng song song có nghĩa là các em sẽ tiến hành chứng minh mặt phẳng thứ nhất chứa 2 đường thẳng cắt nhau lần lượt song song với mặt phẳng còn lại.
Dạng 13: Thiết diện cắt bởi một mặt phẳng song song với một mặt phẳng cho trước
Khi gặp dạng toán thiết diện cắt bởi một mặt phẳng song song với một mặt phẳng cho trước, các em hãy sử dụng định lý: “Nếu hai mặt phẳng song song bị cắt bởi một mặt phẳng thứ ba thì 2 giao tuyến song song nhau.“
Nguồn: Hình Học Không Gian – Marathon Education
- Cách 1: Tìm 2 điểm chung giữa hai mặt phẳng
Tổng Hợp 13 Dạng Hình Học Không Gian Thường Gặp Và Cách Giải
Hình học không gian vẫn luôn là một trong những dạng toán làm khó nhiều thế hệ học sinh. Bên cạnh việc nắm vững lý thuyết, các em còn phải biết cách vẽ hình thật chuẩn xác thì mới có thể giải quyết được loại bài tập hóc búa này. Để giúp các em nắm vững […]
Đã cập nhật 17 tháng 2 năm 2022
Bởi TopOnMedia
Tags:
Marathon