Lũy thừa và hàm số lũy thừa đã không còn xa lạ với chương trình Toán giải tích lớp 12. Kiến thức này thường xuất hiện trong các bài toán về khảo sát hàm số. TheTips sẽ giúp các em hiểu rõ hơn về khái niệm lũy thừa cũng như đạo hàm của hàm số lũy thừa qua bài viết sau.
Khái niệm lũy thừa
Các em hãy cùng Marathon tìm hiểu rõ hơn về khái niệm lũy thừa với từng loại số mũ dưới đây.
Lũy thừa với số mũ nguyên
Định nghĩa: Cho một số nguyên dương n bất kỳ và một số thực a tùy ý. Lũy thừa bậc n của số a là tích của n thừa số a và có dạng
\begin{aligned}
&a^n=a.a.a.....a \ \text{(n thừa số a)}\\
&\text{Với } a \not = 0 \text{ thì } a^0=1, \ a^{-n}=\frac{1}{a^n}
\end{aligned}Lưu ý: 0n và 0-n không có nghĩa.
Tính chất: Lũy thừa với số mũ nguyên sẽ có tính chất tương tự như lũy thừa với số mũ nguyên dương.
Lũy thừa với số mũ hữu tỉ
\begin{aligned}
&\footnotesize\text{Cho một số thực dương a bất kỳ và r là một số hữu tỉ có dạng }r=\frac{m}{n}\\
&\footnotesize\text{Trong đó m là một số nguyên còn n là một số nguyên lớn hơn 1. Lúc này, }\\
&\footnotesize\text{lũy thừa của a với số mũ r và số }a^r
\footnotesize\text{ xác định bởi:}\\
&a^r=a^\frac{m}{n} =\sqrt[n]{a^m}\\
&\footnotesize\text{Đặc biệt: Khi }m=1\ \text{thì} \ a^\frac{1}{n}=\sqrt[n]{a}
\end{aligned}Lũy thừa với số mũ thực
Cho a, b là những số thực dương và α, β là những số thực dương tùy ý. Khi đó ta có các tính chất của lũy thừa với số mũ thực như sau:
\begin{aligned}
&a^α.a^β=a^{α+β}\\
&\frac{a^α}{a^β}=a^{α-β}\\
&(a^α)^β=a^{αβ}\\
&(ab)^α=a^α.b^α\\
&\left( \frac{a}{b}\right)^α=\frac{a^α}{b^α}\\
& \text{Nếu }a>1\text{ thì } a^α>a^β \Leftrightarrow α>β\\
& \text{Nếu }aa^β \Leftrightarrow αHàm số lũy thừa là gì?
Những hàm số có dạng y=xα (α ∈ R) được gọi là hàm số lũy thừa. Tùy thuộc vào α mà mỗi hàm số sẽ có những tập xác định khác nhau:
- Nếu α nguyên dương thì tập xác định là R.
- Nếu α nguyên âm hoặc α = 0 thì tập xác định là R∖{0}.
- Nếu α không nguyên thì tập xác định là (0;+∞).
Đạo hàm của hàm số lũy thừa
Với số mũ tổng quát
\begin{aligned}
&\footnotesize\text{Hàm số y}=x^\alpha \text{ có đạo hàm tại mọi }x\in(0;+\infin) \text{ và y'}=(x^\alpha)'=\alpha x^{\alpha-1}.\\
&\footnotesize\text{Nếu hàm số u = u(x) nhận giá trị dương và có đạo hàm trong khoảng J thì }\\
&\footnotesize\text{hàm số } y=u^\alpha(x) \text{ cũng có đạo hàm trên J là:}\\
&y'=[u^\alpha(x)]^{-1}=\alpha x^{\alpha-1}.(x).u'(x)
\end{aligned}Với số mũ nguyên dương
Trong trường hợp số mũ nguyên dương, hàm số y = xn có tập xác định R và có đạo hàm trên toàn trục số. công thức tính đạo hàm hàm số lũy thừa có thể được mở rộng thành:
\begin{aligned}
&\forall x \in \R, \ (x^n)'=nx^{n-1}\\
&\forall x \in J,\ [u^n(x)]'=nu^{n-1} \ (x) \ u'(x) \\
&\text{(nếu u=u(x) có đạo hàm trong khoảng J)}
\end{aligned}Với số mũ nguyên âm
Nếu số mũ là số nguyên âm thì hàm số y=xn có tập xác định là R{0} và có đạo hàm tại mọi x khác 0, công thức đạo hàm hàm số lũy thừa tổng quát được mở rộng thành:
\begin{aligned}
& \forall x \not=0, (x^n)'=nx^{n-1}\\
&\forall x \in J, [u^n(x)]'=nu^{n-1}.(x).u'(x)\\
&\text{(nếu u=u(x) } \not= 0 \text{ có đạo hàm trong khoảng J)}
\end{aligned}Đạo hàm của căn thức
\begin{aligned}
&\footnotesize\text{Hàm số }y=\sqrt[n]{x}\text{ có thể được xem như là dạng mở rộng của hàm số lũy thừa }\\
&\footnotesize y=x^\frac{1}{n} \text{ (tập xác định của }y=\sqrt[n]{x}\text{ chứa tập xác định của }y=x^\frac{1}{n} \text{ và trên tập}\\
&\footnotesize\text{xác định của }y=x^\frac{1}{n}\text{thì hai hàm số trùng nhau).}\\
&\footnotesize \text{Công thức tính đạo hàm căn thức:}\\
&\footnotesize y=\sqrt[n]{x}=x^\frac{1}{n} \text{\ \ \ \ và\ \ \ \ } (x^\frac{1}{n})'=\frac{1}{n}x^{\frac{1}{n}-1}\\
&\footnotesize \Rightarrow (\sqrt[n]{x})'=\frac{1}{n\sqrt[n]{x^{n-1}}}\\
&\footnotesize \Rightarrow (\sqrt[n]{u(x)})'=\frac{u'(x)}{n\sqrt[n]{u^{n-1}(x)}}\\
\end{aligned}Sự biến thiên và đồ thị của hàm số lũy thừa trên khoảng (0; +∝):
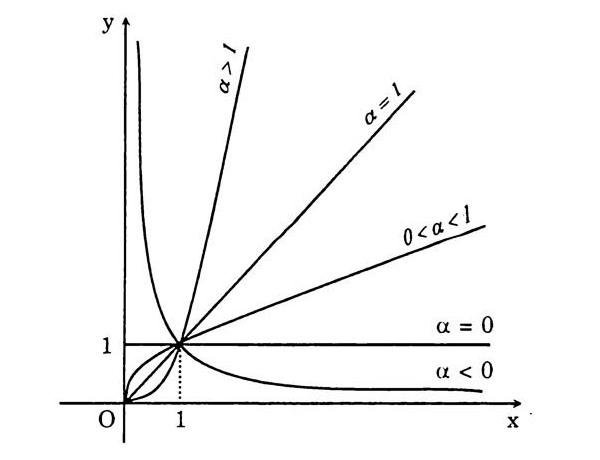
Tính chất của hàm số lũy thừa trên khoảng (0; +∝):
- Đồ thị luôn đi qua điểm (1;1).
- Khi α>0 hàm số luôn đồng biến, khi α
- Đồ thị của hàm số không có tiệm cận khi α > 0. Khi α
Chú ý: Khi khảo sát hàm số y= xα với α cụ thể thì cần xét hàm số trên toàn bộ tập xác định của nó chứ không phải chỉ xét riêng trên khoảng (0; +∝).
Nguồn: Hàm Số Lũy Thừa – Marathon Education









