Bảng Tổng Hợp Các Kí Hiệu Trong Toán Học Phổ Biến

Các em thân mến, các kí hiệu trong toán học có rất nhiều. Việc ghi nhớ các kí hiệu này sẽ giúp các em hiểu rõ ý nghĩa và hoàn thành bài tập toán nhanh chóng. Đặc biệt, việc sử dụng các kí hiệu khi tóm tắt, hệ thống hóa công thức sẽ giúp việc ghi nhớ dễ dàng hơn. Vì vậy, TheTips đã thực hiện biên soạn “bảng tổng hợp các kí hiệu trong toán học” gửi đến các em trong bài viết sau.

Giới thiệu về các kí hiệu trong toán học

Bộ môn Toán phụ thuộc nhiều vào các con số và ký hiệu. Các kí hiệu trong toán học được sử dụng để thực hiện các phép toán. Mỗi kí hiệu toán học vừa đại diện cho một đại lượng, vừa biểu thị mối quan hệ giữa các đại lượng.

Ví dụ: 

• Số Pi (π) giữ giá trị 22/7 hoặc 3,17.
• Hằng số điện tử hay hằng số Euler (e) có giá trị là 2,718281828… 

Bảng tổng hợp các kí hiệu trong toán học phổ biến

TheTips đã tổng hợp các các kí hiệu trong toán học phổ biến như bên dưới. Nội dung này được phân loại rõ ràng để các em tiện theo dõi và sử dụng trong quá trình học tập môn Toán.

Bảng tổng hợp các kí hiệu cơ bản

Dưới đây là bảng thông tin về những kí hiệu toán cơ bản thường được sử dụng mà TheTips tổng hợp được.

Bảng tổng hợp các kí hiệu đại số 

Tiếp theo, TheTips sẽ chia sẻ cho các em những thông tin về những kí hiệu đại số phổ biến.

Bảng tổng hợp các kí hiệu hình học 

Cùng với đại số, TheTips sẽ giới thiệu đến các em những kí hiệu hình học thường được sử dụng.

Biểu tượng	Tên ký hiệu	Ý nghĩa	Ví dụ
∠	kí hiệu góc	hình thành bởi hai tia	∠ABC = 30 °
∡	kí hiệu góc		ABC = 30 °
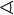
	kí hiệu góc hình cầu	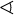	AOB = 30 °
∟	kí hiệu góc vuông	= 90 °	α = 90 °
°	độ	1 vòng = 360 °	α = 60 °
deg	độ	1 vòng = 360deg	α = 60deg
′	dấu ngoặc đơn	phút, 1° = 60′	α = 60°59 ′
″	dấu ngoặc kép	giây, 1′ = 60″	α = 60°59′59″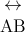
	hàng	dòng vô hạn
AB	đoạn thẳng	đoạn thẳng từ điểm A đến điểm B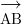
	tia	tia bắt đầu từ điểm A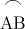
	vòng cung	cung từ điểm A đến điểm B	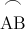= 60 °
⊥	kí hiệu vuông góc	đường vuông góc (góc 90 °)	AC ⊥ BC
∥	kí hiệu song song	những đường thẳng song song	AB ∥ CD
≅	kí hiệu tương đẳng	hai hình có cùng hình dạng và kích thước	∆ABC≅ ∆XYZ
~	kí hiệu giống nhau	hình dạng giống nhau, không cùng kích thước	∆ABC ~ ∆XYZ
Δ	kí hiệu tam giác	Hình tam giác	ΔABC≅ ΔBCD
|x – y|	khoảng cách	khoảng cách giữa các điểm x và y	|x – y| = 5
π	hằng số pi	π = 3,141592654 … là tỷ số giữa chu vi và đường kính của hình tròn	c = π⋅d = 2⋅π⋅r
rad	radian	đơn vị góc radian	360° = 2π rad
c	radian	đơn vị góc radian	360° = 2πc
grad	gradian	đơn vị góc gradian	360° = 400 grad
g	gradian	đơn vị góc gradian	360° = 400g

Bảng tổng hợp các kí hiệu xác suất và thống kê

Xác suất và thống kê không chỉ phổ biến trong chương trình phổ thông mà còn ứng dụng khá nhiều trong cuộc sống. Do đó, các em cũng nên biết thêm kiến thức về những kí hiệu xác suất và thống kê thường được sử dụng bên dưới.

Biểu tượng	Tên ký hiệu	Ý nghĩa	Ví dụ
P (A)	hàm xác suất	xác suất của biến cố A	P (A) = 0,5
P (A ⋂ B)	xác suất các sự kiện giao nhau	xác suất của biến cố A và B	P (A ⋂ B) = 0,5
P (A ⋃ B)	xác suất của sự kiện hợp nhau	xác suất của biến cố A hoặc B	P (A ⋃ B) = 0,5
P (A | B)	hàm xác suất có điều kiện	xác suất của biến cố A, biết rằng biến cố B đã xảy ra	P (A | B) = 0,3
f (x)	hàm mật độ xác suất (pdf)	P (a ≤ x ≤ b) = ∫f(x)dx
F (x)	hàm phân phối tích lũy (cdf)	F (x) = P (X ≤ x)
μ	ký hiệu bình quân	bình quân của quần thể	μ = 10
E  (X)	giá trị kỳ vọng	giá trị kỳ vọng của biến ngẫu nhiên X	E (X) = 10
E ( X | Y )	giá trị kỳ vọng có điều kiện	giá trị kỳ vọng của biến ngẫu nhiên X, biết rằng biến Y đã xảy ra	E (X | Y = 2) = 5
var (X)	phương sai	phương sai của biến ngẫu nhiên X	var (X) = 4
σ 2	phương sai	phương sai của các giá trị trong quần thể	σ 2 = 4
std(X)	độ lệch chuẩn	độ lệch chuẩn của biến ngẫu nhiên X	std (X) = 2
σX	độ lệch chuẩn	giá trị độ lệch chuẩn của biến ngẫu nhiên X	σX  = 2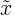
	số trung vị	giá trị ở giữa của biến ngẫu nhiên x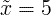
cov(X, Y)	hiệp phương sai	hiệp phương sai của các biến ngẫu nhiên X và Y	cov(X, Y) = 4
corr (X, Y)	hệ số tương quan	hệ số tương quan của các biến ngẫu nhiên X và Y	corr (X, Y) = 0,6
ρX, Y	ký hiệu tương quan	ký hiệu tương quan của các biến ngẫu nhiên X và Y	ρX, Y = 0,6
∑	kí hiệu tổng	tổng – tổng của tất cả các giá trị trong phạm vi của chuỗi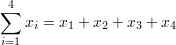
∑∑	tổng kết kép	tổng kết kép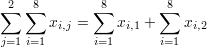
Mo	số yếu vị	giá trị xuất hiện thường xuyên nhất trong dãy số
MR	khoảng giữa	MR = (xtối đa + xtối thiểu)/2
Md	số trung vị mẫu	một nửa quần thể thấp hơn giá trị này
Q1	hạ vị/ phần tư đầu tiên	25% quần thể thấp hơn giá trị này
Q 2	trung vị / phần tư thứ hai	50% quần thể thấp hơn giá trị này = số trung vị của các mẫu
Q 3	thượng vị/ phần tư thứ ba	75% quần thể thấp hơn giá trị này
x	trung bình mẫu	trung bình/ trung bình cộng	x = (2 + 5 + 9)/3 = 5.333
s2	phương sai mẫu	công cụ ước tính phương sai của các mẫu trong quần thể	s2 = 4
s	độ lệch chuẩn mẫu	ước tính độ lệch chuẩn của các mẫu trong quần thể	s = 2
zx	điểm chuẩn	zx = (x – x)/ sx
X ~	phân phối của X	phân phối của biến ngẫu nhiên X	X ~ N (0,3)
N (μ, σ 2)	phân phối chuẩn	phân phối gaussian	X ~ N (0,3)
Ư (a, b)	phân bố đồng đều	xác suất bằng nhau trong phạm vi a, b	X ~ U (0,3)
exp (λ)	phân phối theo cấp số nhân	f (x) = λe– λx, x ≥0
gamma (c, λ)	phân phối gamma	f (x) = λ cx c-1 e – λx / Γ (c), x ≥0
χ2 (k)	phân phối chi bình phương	f (x) = xk / 2-1e– x/2 / (2 k/2 Γ (k/2))
F (k1, k2)	Phân phối F
Bin (n, p )	phân phối nhị thức	f(k) = nCkpk(1-p)nk
Poisson (λ)	Phân phối Poisson	f(k) = λke– λ/k !
Geom (p)	phân bố hình học	f (k) = p(1-p)k
HG (N, K, n)	phân bố siêu hình học
Bern (p)	Phân phối Bernoulli

Bảng tổng hợp các kí hiệu tập hợp 

Đây là những ký hiệu lý thuyết liên quan đến tập hợp phổ biến mà các em thường gặp.

Biểu tượng	Tên ký hiệu	Ý nghĩa	Ví dụ
{}	tập hợp	một tập hợp các yếu tố	A = {3,7,9,14},B = {9,14,28}
A ∩ B	giao	các đối tượng thuộc tập A và tập hợp B	A ∩ B = {9,14}
A ∪ B	liên hợp	các đối tượng thuộc tập hợp A hoặc tập hợp B	A ∪ B = {3,7,9,14,28}
A ⊆ B	tập hợp con	A là một tập con của B. Tập hợp A nằm trong tập hợp B.	{9,14,28} ⊆ {9,14,28}
A ⊂ B	tập hợp con chính xác/ tập hợp con nghiêm ngặt	A là một tập con của B, nhưng A không bằng B.	{9,14} ⊂ {9,14,28}
A ⊄ B	không phải tập hợp con	tập A không phải là tập con của tập B	{9,66} ⊄ {9,14,28}
A ⊇ B	tập chứa	A là tập chứa của B. Tập A bao gồm tập B	{9,14,28} ⊇ {9,14,28}
A ⊃ B	tập chứa chính xác / tập chứa nghiêm ngặt	A là tập chứa của B, nhưng B không bằng A.	{9,14,28} ⊃ {9,14}
A ⊅ B	không phải tập chứa	tập hợp A không phải là tập chứa của tập hợp B	{9,14,28} ⊅ {9,66}
2A	tập lũy thừa	tất cả các tập con của A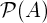
	tập lũy thừa	tất cả các tập con của A
A = B	bằng nhau	cả hai tập đều có các phần tử giống nhau	A = {3,9,14},B = {3,9,14},A = B
Ac	phần bù	tất cả các đối tượng không thuộc tập A
A B	phần bù tương đối	đối tượng thuộc về A và không thuộc về B	A = {3,9,14},B = {1,2,3},A B = {9,14}
A – B	phần bù tương đối	đối tượng thuộc về A và không thuộc về B	A = {3,9,14},B = {1,2,3},A – B = {9,14}
A ∆ B	sự khác biệt đối xứng	các đối tượng thuộc tập hợp A hoặc tập hợp B nhưng không thuộc giao điểm của chúng	A = {3,9,14},B = {1,2,3},A ∆ B = {1,2,9,14}
A ⊖ B	sự khác biệt đối xứng	các đối tượng thuộc tập hợp A hoặc tập hợp B nhưng không thuộc giao điểm của chúng	A = {3,9,14},B = {1,2,3},A ⊖ B = {1,2,9,14}
a ∈ A	thuộc	phần tử của tập hợp	A = {3,9,14}, 3 ∈ A
x ∉ A	không thuộc	không phải là phần tử của tập hợp	A = {3,9,14}, 1 ∉ A
(a, b)	cặp được sắp xếp theo thứ tự	tập hợp của 2 yếu tố
A × B	Tích Descartes	tập hợp tất cả các cặp được sắp xếp từ A và B	A×B = {(a,b) | a∈A, b∈B}
|A|	lực lượng	số phần tử của tập A	A = {3,9,14}, |A| = 3
#A	lực lượng	số phần tử của tập A	A = {3,9,14}, # A = 3
|	thanh dọc	như vậy mà	A = {x|3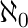
	aleph-null	tập hợp số tự nhiên vô hạn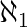
	aleph-one	tập hợp số tự nhiên có thể đếm được
Ø	tập hợp rỗng	Ø = {}	C = {Ø}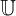
	tập hợp phổ quát	tập hợp tất cả các giá trị có thể có được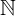
0	tập hợp số tự nhiên / số nguyên (với số 0)	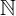0 = {0,1,2,3,4, …}	0 ∈ 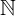0
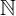1	tập hợp số tự nhiên / số nguyên (không có số 0)	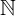1 = {1,2,3,4,5, …}	6 ∈ 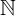1
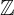
	tập hợp số nguyên	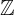= {…- 3, -2, -1,0,1,2,3, …}	-6 ∈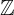
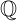
	tập hợp số hữu tỉ	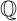= { x | x = a / b , a , b ∈ 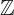}	2/6 ∈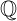
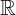
	tập hợp số thực	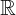= { x | -∞ x	6.343434∈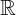
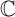
	tập hợp số phức	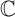= { z | z = a + bi , -∞ a b	6 + 2 i ∈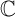

Nguồn: Các Kí Hiệu Trong Toán Học – Marathon Education